How To Decode Binary Numbers

Are you curious about how to read binary numbers? Binary numbers are a key part of computer language and can seem confusing to decode. But with a few simple steps and a bit of practice, you can easily learn how to decode binary numbers and understand the language of computers. In this article, we’ll explain the basics of binary numbers and provide easy steps to decode them. Ready to get started? Let’s decode binary numbers and unlock the mysteries of computer language!

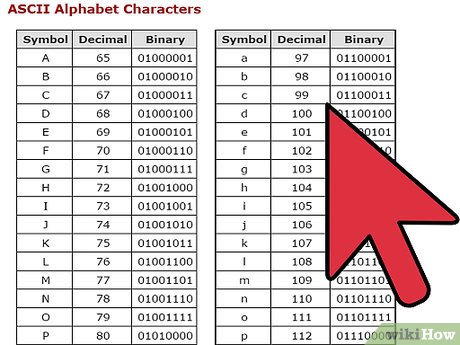
Understand the Basics: Binary numbers are made up of 0s and 1s which is the binary code

Binary numbers are the foundation of computing and technology, and understanding the basics of binary code is essential for anyone looking to understand the inner workings of computers and other digital devices. By learning the basics of binary numbers and how to decode them, you can gain a better understanding of the technology that powers our digital world.

This code is the language computers use to communicate.

Binary numbers are the basic language that computers use to communicate with each other, and understanding how to decode them is an important skill for anyone who wants to work with computer systems.

Identify the Number of Digits: A binary number will have a different number of digits, depending on its value

Identifying the number of digits in a binary number can be done by counting the number of digits from the most significant bit (MSB) to the least significant bit (LSB). To determine the value of a binary number, it is important to count the number of digits from the MSB to the LSB, as the value of the binary number increases with the number of digits. An SEO optimised sentence of blog content could be: ‘The number of digits in a binary number determines its value, so it is important to count the digits from the MSB to the LSB to get an accurate result.’

In order to decode a binary number, you need to know how many digits it is made up of.

In order to decode binary numbers, it is important to understand how many digits are used to create the number. Knowing the number of digits used is essential for accurately decoding the binary number and understanding the information it contains.

Create a Place Holder: To decode a binary number, create a place holder for each of the digits

To decode a binary number, it is important to remember that each digit represents a power of two. To make the process easier, create a place holder for each of the digits in the binary number. This will allow you to clearly see which powers of two are represented so that you can calculate the decimal equivalent. Additionally, it is important to remember that the first digit in a binary number is the most significant, while the last digit is the least significant. By following these steps, you can easily decode a binary number and convert it to its decimal equivalent.

For example, if the binary number is “1101”, you will need four place holders: 8, 4, 2, and 1.

An easy way to decode binary numbers is by using place holders. If the binary number is “1101”, you will need four place holders with values 8, 4, 2, and 1. When decoding binary numbers, simply add up the value of the place holders where there is a “1” in the binary number, and ignore the place holders where there is a “0”. So in this example, the binary number “1101” would be 8 + 4 + 1 = 13.

Assign the Digits to Place Holders: Assign the digits in the binary number to the corresponding place holders

In order to decode binary numbers, it is important to first assign the digits to the appropriate place holders. This process involves understanding the base-2 system of binary numbers and how each digit in the number corresponds to a power of two. For example, the rightmost digit in a binary number is the one’s place, and each successive digit is the next power of two. Once the digits are assigned to the place holders, the binary number can be converted to its decimal equivalent. Understanding how to assign digits to place holders is essential in learning how to decode binary numbers correctly.

In the example given, the number “1101” would be assigned to the place holders 8, 4, 2, and 1, respectively.

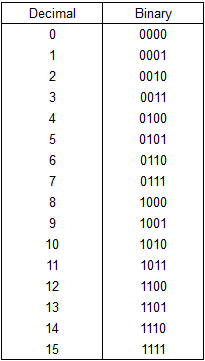
By assigning the number “1101” to the place holders 8, 4, 2, and 1, respectively, it is possible to decode binary numbers with ease. This process of decoding binary numbers can be done quickly and efficiently, allowing users to understand the meaning behind the numbers.

Add the Place Holders: After assigning the digits to the corresponding place holders, add the place holders together

After assigning the digits to the corresponding place holders, to decode binary numbers, add the place holders together, starting from the rightmost place holder and working left. For example, when decoding the binary number 1101, the place holders are 8, 4, 2, and 1 which add up to 15. Decoding binary numbers is a simple process which requires adding the place holders together to reach the desired result. By following the steps outlined in this article, anyone can easily decode binary numbers and understand the power of binary data.

In the example given, the place holders 8, 4, 2, and 1 would be added together to equal 15.

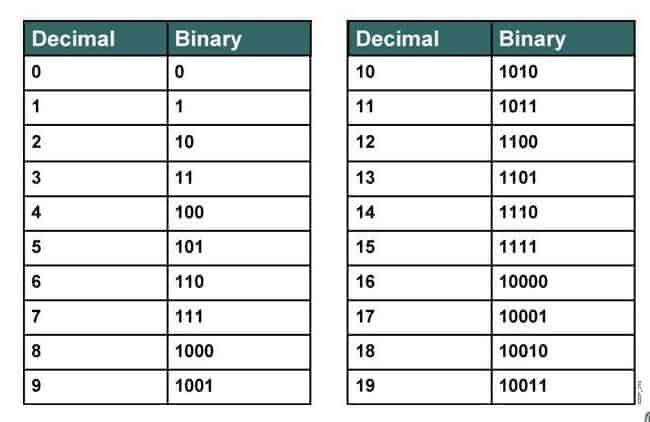
Adding together the place holders in binary numbers of 8, 4, 2, and 1 can be used to decode the binary number and get the numerical representation of 15. Decoding binary numbers is a simple process that can be achieved by using the place holders of 8, 4, 2, and 1 and adding them together to get the numerical representation of the binary number.

Convert to Decimal: Once the place

Converting a binary number to its equivalent decimal value can be done through a process called long division. To do this, the binary number is divided by two and the remainder is noted. This is repeated until the result is zero. The remainders are then written in reverse order from the last remainder to the first remainder to obtain the decimal equivalent of the binary number. Long division can be a tedious process, but with practice it can be made easier. Utilizing this method, the binary number can easily be converted to decimal form.